Find a Hardware Injection: Step 2
This tutorial will pick up where step 1 left off. If you haven't already completed step 1, you may want to do that first.
Working in the frequency domain
A match-filter search requires 3 frequency domain functions: the data, the power-spectral density (PSD) of the expected noise, and a template representing the expected signal. In this step, we'll assemble each of these 3 pieces.
Make a template
We can generate a template for the signal using a Post-Newtonian aproximation, as described in Allen et. al (2011). An implementation of this is available in the module template.py. Download template.py to your working directory, and you can generate a template like this:
# -- Make a frequency domain template
import template
temp, temp_freq = template.createTemplate(fs, seg_time, 10, 10)
This will produce an frequency domain inspiral template, and store the result
in the numpy array temp. The template will be an inspiral signal
for a compact object merger where each has a mass of 10 solar masses.
The LIGO noise is very high at low frequencies, so we want to remove these from our search by setting the template to 0 at low frequencies.
temp[temp_freq < 25] = 0To get a sense of how the template depends on frequency, let's plot the magnitude of the template as a function of frequency:
plt.figure()
plt.loglog(temp_freq, abs(temp))
plt.axis([10, 1000, 1e-22, 1e-19])
plt.xlabel("Frequency (Hz)")
plt.ylabel("Template value (Strain/Hz")
plt.grid()
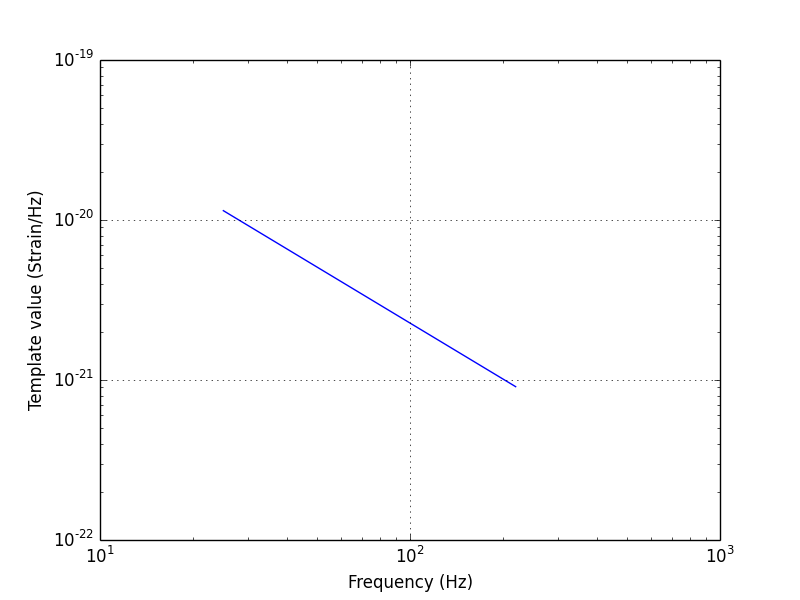
Notice that the template has more power at lower frequencies. This is because inspiraling compact objects lose energy more slowly when they are far apart, and so spend more time in slower moving orbits than faster orbits.
Fourier Transform the Data
Since the data is a real time series, we can use the numpy function fft.rfft, which computes a real Fast Fourier Transform (FFT). Before we do this, we'll need to window the data to minimize edge effects.
window = np.blackman(inj_data.size)
data_fft = np.fft.rfft(inj_data*window)Compute the PSD
We already marked a section of data that we plan to use to aproximate the
power in the noise. We can use the matplotlib function psd
to compute the PSD. By setting NFFT equal to the size of the data segment, we
guarentee that the frequency domain data and PSD will have the same number of
samples.
Pxx, psd_freq = mlab.psd(noise_data, Fs=fs, NFFT=len(inj_data))
What's next?
Now that we have the data, the noise, and the template all in the frequency domain, we're ready to compute the match-template output. Go on to step 3 to see how this works.
