Plot Gallery

To make any plot shown on this page, start with the following code to read the strain data and data quality information from the LIGO data file that you downloaded in step 1 of the introductory tutorial. readligo refers to the sample reader functions described in step 4, which read data from a LIGO data file:

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
import readligo as rl

fileName = 'H-H1_LOSC_4_V1-815411200-4096.hdf5'
strain, time, channel_dict = rl.loaddata(fileName)
ts = time[1] - time[0]      #-- Time between samples
fs = int(1.0 / ts)          #-- Sampling frequency

#-- Choose a few seconds of "good data"
segList = rl.dq_channel_to_seglist(channel_dict['DEFAULT'], fs)
length = 16  # seconds
strain_seg = strain[segList[0]][0:(length*fs)]
time_seg = time[segList[0]][0:(length*fs)]

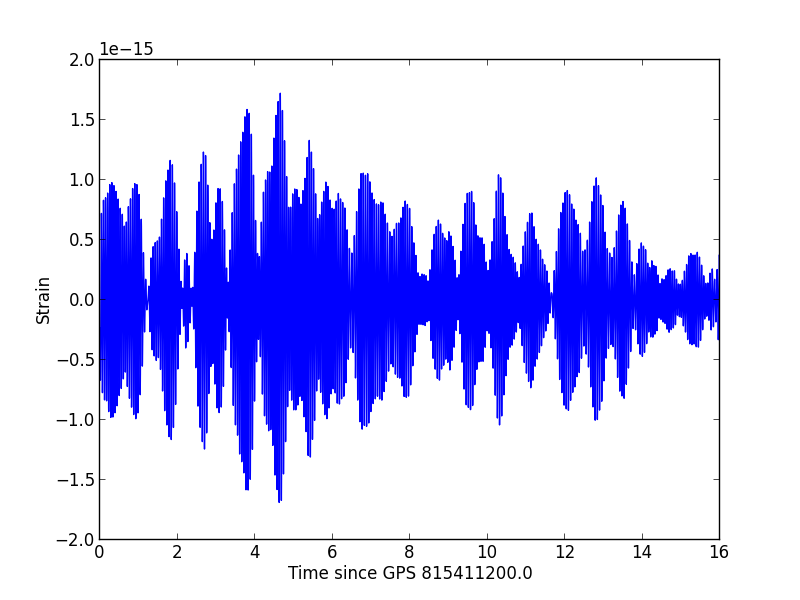
Plot the time series

The strain time series, or h(t). This is the most direct plot of LIGO data. The time series is dominated by low frequency noise, which appears as smooth oscillations at around 20 Hz.

Show the code

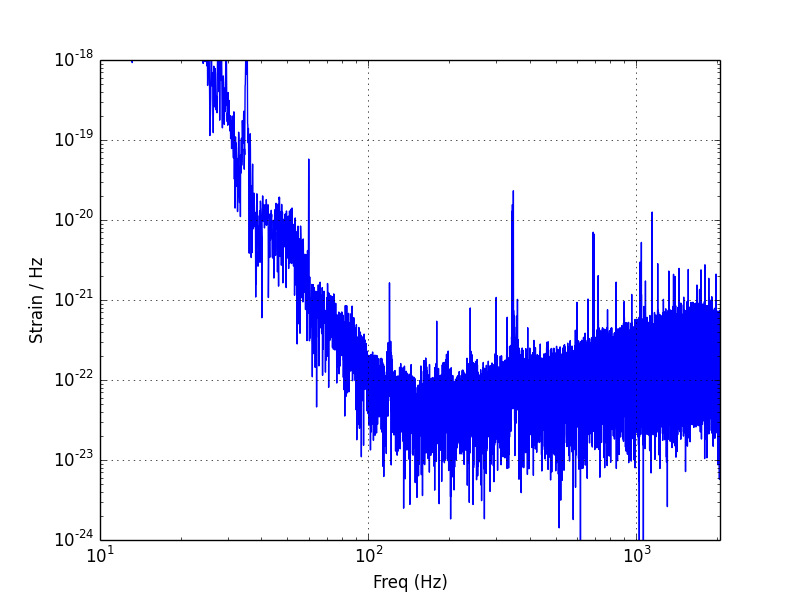
FFT with Blackman Window

A Fast Fourier Transform, or FFT, is one method to transform the data into the frequency domain. Here, we first apply a Blackman Window to force the data to zero at the time boudaries, and so reduce edge effects in the FFT. The LIGO noise spectrum is seen to have the most power at low frequencies (f < 50 Hz), due mainly to seismic noise. The most sesitive band, often called "The Bucket", is roughly 100 - 300 Hz.

Show the code

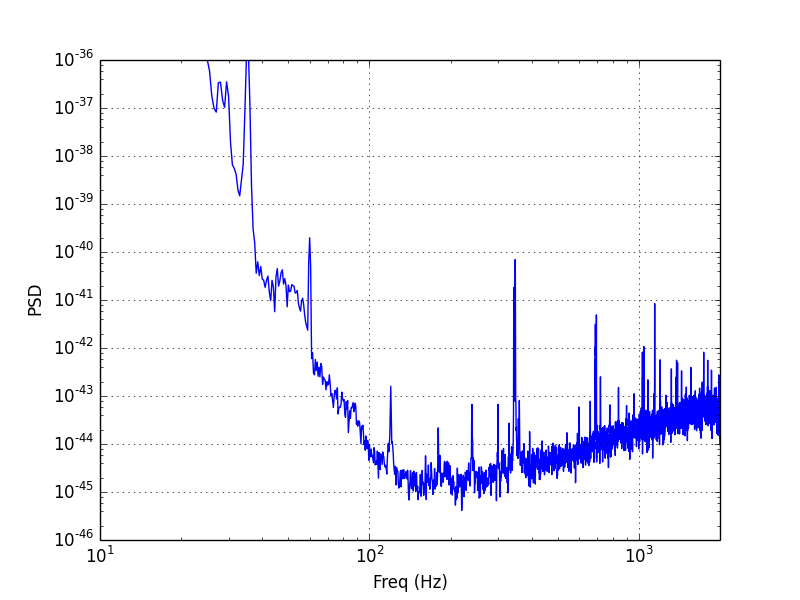
Power Spectral Density (PSD)

The Power Spectral Density is another representation of how the power in the data is distributed in frequency space. Matplotlib's psd method use's Welch's method to estimate the PSD. The method divides the data into segments with NFFT samples, computes a periodogram of each segment (similar to the FFT plotted above), and then takes the time average of the periodograms. This averaging over several segments reduces the variance in the result, which is why the PSD looks "thinner" than the FFT.

Show the code

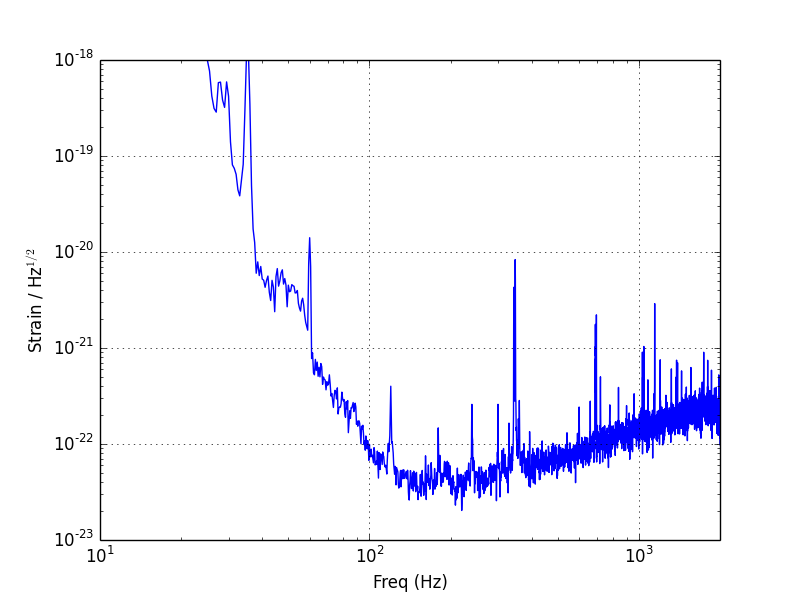
Amplitude Spectral Density (ASD)

The ASD can be obtained by taking the square root of the PSD. This is done to give units that can be more easily compared with the time domain data or FFT. More information about the LIGO ASD can be seen on the Instrumental Lines page.

Show the code

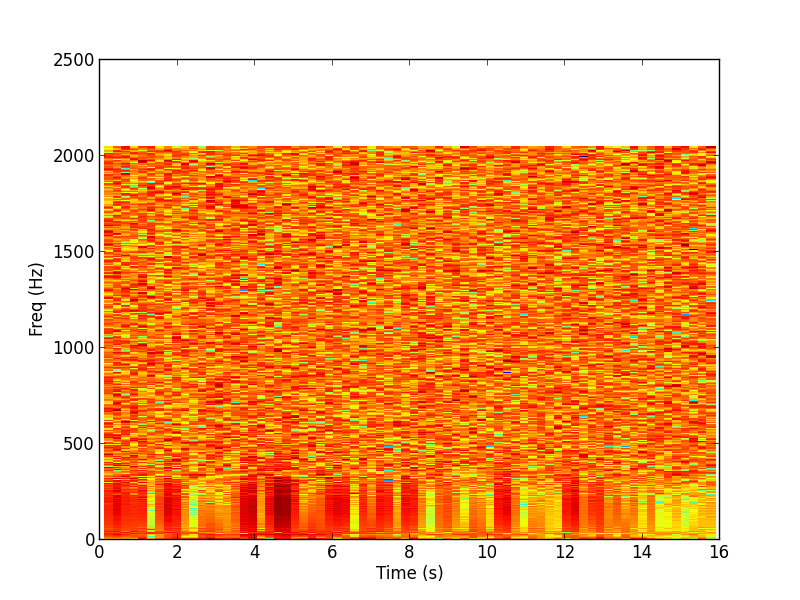
Spectrogram

This spectrogram shows how the PSD of the data varies as a function of time. The main feature we see is that the low frequencies contain more power than the high frequencies, as in the above plots.

Show the code

Spectrogram renormalized to the median power in each frequency bin

In this spectrogram, the power in each frequency bin has been normalized by the median power for that bin. This "whitens" the data. The remaining spectrogram shows how the power fluctuates in time. Such whitened spectrograms are useful for visualizing transient signals. For example, this simulated inspiral is plotted using a technique similar to a whitened spectrogram. You can also see how to visualize a Burst hardware injection in the "Find a Burst Injection" tutorial.

Show the code